Applicant
Prof. Dr. Ulrich Rüde
Computer Science 10 – System simulation (LSS)
Friedrich-Alexander-Universität Erlangen-Nürnberg
Project Overview
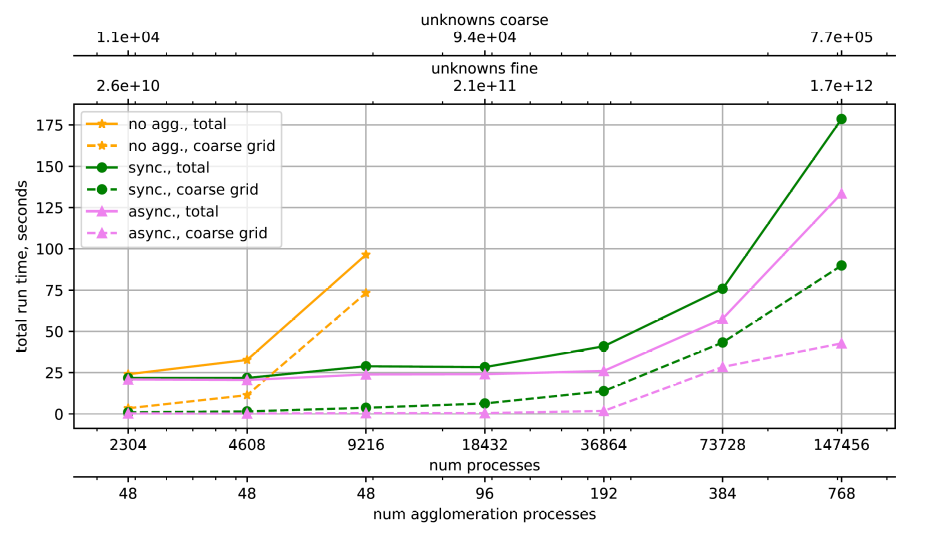
During this project, we developed a scalable implementation of synchronous and asynchronous agglomeration for a massively parallel multigrid solver in the HyTeG finite element framework. HyTeG is for example used for geophysical applications like earth mantle convection modelling (https://terraneo.fau.de/).
The asynchronous agglomeration technique performs the factorization of the coarse grid system matrix during the recursive descent of the multigrid cycle. We apply the multigrid solver to the Stokes problem and demonstrate the flexibility of the agglomeration implementation through application to an iterative, AMG-preconditioned Krylov-type coarse-grid solver and a sparse direct method.
The implementation prevents the communication cost of the coarse grid solver to blow up in simulations with a few hundred compute nodes. In suitable configurations, the asynchronous agglomeration hides the factorization entirely without increasing the run time of the remaining multigrid iteration. We present results of a scalability benchmark, solving linear systems with more than a trillion (10^12) unknowns on more than 140.000 parallel processes (cf. figure).